{
"cells": [
{
"cell_type": "markdown",
"id": "2165e3f2",
"metadata": {},
"source": [
"# Markov Chains: Irreducibility and Ergodicity\n",
"\n",
"\n",
"<a id='index-0'></a>\n",
"In addition to what’s in Anaconda, this lecture will need the following libraries:"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "2eb775b4",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"!pip install quantecon"
]
},
{
"cell_type": "markdown",
"id": "25288fa1",
"metadata": {},
"source": [
"## Overview\n",
"\n",
"This lecture continues on from our [earlier lecture on Markov chains](https://intro.quantecon.org/markov_chains_I.html).\n",
"\n",
"Specifically, we will introduce the concepts of irreducibility and ergodicity, and see how they connect to stationarity.\n",
"\n",
"Irreducibility describes the ability of a Markov chain to move between any two states in the system.\n",
"\n",
"Ergodicity is a sample path property that describes the behavior of the system over long periods of time.\n",
"\n",
"As we will see,\n",
"\n",
"- an irreducible Markov chain guarantees the existence of a unique stationary distribution, while \n",
"- an ergodic Markov chain generates time series that satisfy a version of the\n",
" law of large numbers. \n",
"\n",
"\n",
"Together, these concepts provide a foundation for understanding the long-term behavior of Markov chains.\n",
"\n",
"Let’s start with some standard imports:"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "999ea716",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"import matplotlib.pyplot as plt\n",
"import quantecon as qe\n",
"import numpy as np"
]
},
{
"cell_type": "markdown",
"id": "fccd37ca",
"metadata": {},
"source": [
"\n",
"<a id='mc-irreducible'></a>"
]
},
{
"cell_type": "markdown",
"id": "8689fae9",
"metadata": {},
"source": [
"## Irreducibility\n",
"\n",
"To explain irreducibility, let’s take $ P $ to be a fixed stochastic matrix.\n",
"\n",
"State $ y $ is called **accessible** (or **reachable**) from state $ x $ if $ P^t(x,y)>0 $ for some integer $ t\\ge 0 $.\n",
"\n",
"Two states, $ x $ and $ y $, are said to **communicate** if $ x $ and $ y $ are accessible from each other.\n",
"\n",
"In view of our discussion [above](https://intro.quantecon.org/markov_chains_I.html#finite-mc-mstp), this means precisely\n",
"that\n",
"\n",
"- state $ x $ can eventually be reached from state $ y $, and \n",
"- state $ y $ can eventually be reached from state $ x $ \n",
"\n",
"\n",
"The stochastic matrix $ P $ is called **irreducible** if all states communicate;\n",
"that is, if $ x $ and $ y $ communicate for all $ (x, y) $ in $ S \\times S $."
]
},
{
"cell_type": "markdown",
"id": "b1a248dc",
"metadata": {},
"source": [
"## \n",
"\n",
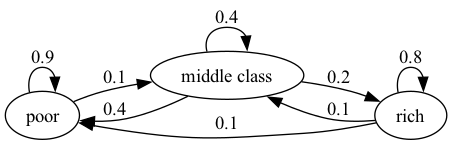
"For example, consider the following transition probabilities for wealth of a\n",
"fictitious set of households\n",
"\n",
"\n",
"\n",
"We can translate this into a stochastic matrix, putting zeros where\n",
"there’s no edge between nodes\n",
"\n",
"$$\n",
"P :=\n",
"\\begin{bmatrix} \n",
" 0.9 & 0.1 & 0 \\\\\n",
" 0.4 & 0.4 & 0.2 \\\\\n",
" 0.1 & 0.1 & 0.8\n",
"\\end{bmatrix}\n",
"$$\n",
"\n",
"It’s clear from the graph that this stochastic matrix is irreducible: we can eventually\n",
"reach any state from any other state.\n",
"\n",
"We can also test this using [QuantEcon.py](http://quantecon.org/quantecon-py)’s MarkovChain class"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "acad2dc9",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"P = [[0.9, 0.1, 0.0],\n",
" [0.4, 0.4, 0.2],\n",
" [0.1, 0.1, 0.8]]\n",
"\n",
"mc = qe.MarkovChain(P, ('poor', 'middle', 'rich'))\n",
"mc.is_irreducible"
]
},
{
"cell_type": "markdown",
"id": "bdcaa5cb",
"metadata": {},
"source": [
"## \n",
"\n",
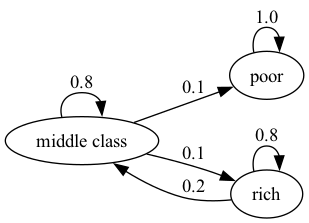
"Here’s a more pessimistic scenario in which poor people remain poor forever\n",
"\n",
"\n",
"\n",
"This stochastic matrix is not irreducible since, for example, rich is not\n",
"accessible from poor.\n",
"\n",
"Let’s confirm this"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "92651d2f",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"P = [[1.0, 0.0, 0.0],\n",
" [0.1, 0.8, 0.1],\n",
" [0.0, 0.2, 0.8]]\n",
"\n",
"mc = qe.MarkovChain(P, ('poor', 'middle', 'rich'))\n",
"mc.is_irreducible"
]
},
{
"cell_type": "markdown",
"id": "1e8c49d7",
"metadata": {},
"source": [
"It might be clear to you already that irreducibility is going to be important\n",
"in terms of long-run outcomes.\n",
"\n",
"For example, poverty is a life sentence in the second graph but not the first.\n",
"\n",
"We’ll come back to this a bit later."
]
},
{
"cell_type": "markdown",
"id": "cd66c593",
"metadata": {},
"source": [
"### Irreducibility and stationarity\n",
"\n",
"We discussed uniqueness of stationary distributions in our earlier lecture [Markov Chains: Basic Concepts](https://intro.quantecon.org/markov_chains_I.html).\n",
"\n",
"There we [stated](https://intro.quantecon.org/markov_chains_I.html#mc_po_conv_thm) that uniqueness holds when the transition matrix is everywhere positive.\n",
"\n",
"In fact irreducibility is sufficient:"
]
},
{
"cell_type": "markdown",
"id": "530a272f",
"metadata": {},
"source": [
"### \n",
"\n",
"If $ P $ is irreducible, then $ P $ has exactly one stationary\n",
"distribution.\n",
"\n",
"For proof, see Chapter 4 of [[Sargent and Stachurski, 2023](https://intro.quantecon.org/zreferences.html#id24)] or\n",
"Theorem 5.2 of [[Häggström, 2002](https://intro.quantecon.org/zreferences.html#id155)].\n",
"\n",
"\n",
"<a id='ergodicity'></a>"
]
},
{
"cell_type": "markdown",
"id": "f85e0f66",
"metadata": {},
"source": [
"## Ergodicity\n",
"\n",
"Under irreducibility, yet another important result obtains:"
]
},
{
"cell_type": "markdown",
"id": "19e40856",
"metadata": {},
"source": [
"## \n",
"\n",
"If $ P $ is irreducible and $ \\psi^* $ is the unique stationary\n",
"distribution, then, for all $ x \\in S $,\n",
"\n",
"\n",
"<a id='equation-llnfmc0'></a>\n",
"$$\n",
"\\frac{1}{m} \\sum_{t = 1}^m \\mathbb{1}\\{X_t = x\\} \\to \\psi^*(x)\n",
" \\quad \\text{as } m \\to \\infty \\tag{35.1}\n",
"$$\n",
"\n",
"Here\n",
"\n",
"- $ \\{X_t\\} $ is a Markov chain with stochastic matrix $ P $ and initial distribution $ \\psi_0 $ \n",
"- $ \\mathbb{1} \\{X_t = x\\} = 1 $ if $ X_t = x $ and zero otherwise. \n",
"\n",
"\n",
"The result in [(35.1)](#equation-llnfmc0) is sometimes called **ergodicity**.\n",
"\n",
"The theorem tells us that the fraction of time the chain spends at state $ x $\n",
"converges to $ \\psi^*(x) $ as time goes to infinity.\n",
"\n",
"\n",
"<a id='new-interp-sd'></a>\n",
"This gives us another way to interpret the stationary distribution (provided irreducibility holds).\n",
"\n",
"Importantly, the result is valid for any choice of $ \\psi_0 $.\n",
"\n",
"The theorem is related to [the law of large numbers](https://intro.quantecon.org/lln_clt.html).\n",
"\n",
"It tells us that, in some settings, the law of large numbers sometimes holds even when the\n",
"sequence of random variables is [not IID](https://intro.quantecon.org/lln_clt.html#iid-violation).\n",
"\n",
"\n",
"<a id='mc-eg1-2'></a>"
]
},
{
"cell_type": "markdown",
"id": "2e155e9c",
"metadata": {},
"source": [
"### Example: ergodicity and unemployment\n",
"\n",
"Recall our cross-sectional interpretation of the employment/unemployment model [discussed before](https://intro.quantecon.org/markov_chains_I.html#mc-eg1-1).\n",
"\n",
"Assume that $ \\alpha \\in (0,1) $ and $ \\beta \\in (0,1) $, so that irreducibility holds.\n",
"\n",
"We saw that the stationary distribution is $ (p, 1-p) $, where\n",
"\n",
"$$\n",
"p = \\frac{\\beta}{\\alpha + \\beta}\n",
"$$\n",
"\n",
"In the cross-sectional interpretation, this is the fraction of people unemployed.\n",
"\n",
"In view of our latest (ergodicity) result, it is also the fraction of time that a single worker can expect to spend unemployed.\n",
"\n",
"Thus, in the long run, cross-sectional averages for a population and time-series averages for a given person coincide.\n",
"\n",
"This is one aspect of the concept of ergodicity.\n",
"\n",
"\n",
"<a id='ergo'></a>"
]
},
{
"cell_type": "markdown",
"id": "09348584",
"metadata": {},
"source": [
"### Example: Hamilton dynamics\n",
"\n",
"Another example is the Hamilton dynamics we [discussed before](https://intro.quantecon.org/markov_chains_I.html#mc-eg2).\n",
"\n",
"Let $ \\{X_t\\} $ be a sample path generated by these dynamics.\n",
"\n",
"Let’s denote the fraction of time spent in state $ x $ over the period $ t=1,\n",
"\\ldots, n $ by $ \\hat p_n(x) $, so that\n",
"\n",
"$$\n",
"\\hat p_n(x) := \\frac{1}{n} \\sum_{t = 1}^n \\mathbb{1}\\{X_t = x\\}\n",
" \\qquad (x \\in \\{0, 1, 2\\})\n",
"$$\n",
"\n",
"The [graph](https://intro.quantecon.org/markov_chains_I.html#mc-eg2) of the Markov chain shows it is irreducible, so\n",
"ergodicity holds.\n",
"\n",
"Hence we expect that $ \\hat p_n(x) \\approx \\psi^*(x) $ when $ n $ is large.\n",
"\n",
"The next figure shows convergence of $ \\hat p_n(x) $ to $ \\psi^*(x) $ when $ x=1 $ and\n",
"$ X_0 $ is either $ 0, 1 $ or $ 2 $."
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "d802046c",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"P = np.array([[0.971, 0.029, 0.000],\n",
" [0.145, 0.778, 0.077],\n",
" [0.000, 0.508, 0.492]])\n",
"ts_length = 10_000\n",
"mc = qe.MarkovChain(P)\n",
"ψ_star = mc.stationary_distributions[0]\n",
"x = 1 # We study convergence to psi^*(x) \n",
"\n",
"fig, ax = plt.subplots()\n",
"ax.axhline(ψ_star[x], linestyle='dashed', color='black', \n",
" label = fr'$\\psi^*({x})$')\n",
"# Compute the fraction of time spent in state 0, starting from different x_0s\n",
"for x0 in range(len(P)):\n",
" X = mc.simulate(ts_length, init=x0)\n",
" p_hat = (X == x).cumsum() / np.arange(1, ts_length+1)\n",
" ax.plot(p_hat, label=fr'$\\hat p_n({x})$ when $X_0 = \\, {x0}$')\n",
"ax.set_xlabel('t')\n",
"ax.set_ylabel(fr'$\\hat p_n({x})$')\n",
"ax.legend()\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"id": "97ee89d1",
"metadata": {},
"source": [
"You might like to try changing $ x=1 $ to either $ x=0 $ or $ x=2 $.\n",
"\n",
"In any of these cases, ergodicity will hold."
]
},
{
"cell_type": "markdown",
"id": "52b51ada",
"metadata": {},
"source": [
"### Example: a periodic chain"
]
},
{
"cell_type": "markdown",
"id": "22c6627d",
"metadata": {},
"source": [
"### \n",
"\n",
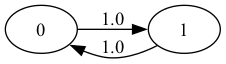
"Let’s look at the following example with states 0 and 1:\n",
"\n",
"$$\n",
"P :=\n",
"\\begin{bmatrix} \n",
" 0 & 1\\\\\n",
" 1 & 0\\\\\n",
"\\end{bmatrix}\n",
"$$\n",
"\n",
"The transition graph shows that this model is irreducible.\n",
"\n",
"\n",
"\n",
"Notice that there is a periodic cycle — the state cycles between the two states in a regular way.\n",
"\n",
"Not surprisingly, this property\n",
"is called [periodicity](https://stats.libretexts.org/Bookshelves/Probability_Theory/Probability_Mathematical_Statistics_and_Stochastic_Processes_%28Siegrist%29/16%3A_Markov_Processes/16.05%3A_Periodicity_of_Discrete-Time_Chains).\n",
"\n",
"Nonetheless, the model is irreducible, so ergodicity holds.\n",
"\n",
"The following figure illustrates"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "31d24f85",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"P = np.array([[0, 1],\n",
" [1, 0]])\n",
"ts_length = 100\n",
"mc = qe.MarkovChain(P)\n",
"n = len(P)\n",
"fig, axes = plt.subplots(nrows=1, ncols=n)\n",
"ψ_star = mc.stationary_distributions[0]\n",
"\n",
"for i in range(n):\n",
" axes[i].axhline(ψ_star[i], linestyle='dashed', lw=2, color='black', \n",
" label = fr'$\\psi^*({i})$')\n",
" axes[i].set_xlabel('t')\n",
" axes[i].set_ylabel(fr'$\\hat p_n({i})$')\n",
"\n",
" # Compute the fraction of time spent, for each x\n",
" for x0 in range(n):\n",
" # Generate time series starting at different x_0\n",
" X = mc.simulate(ts_length, init=x0)\n",
" p_hat = (X == i).cumsum() / np.arange(1, ts_length+1)\n",
" axes[i].plot(p_hat, label=fr'$x_0 = \\, {x0} $')\n",
"\n",
" axes[i].legend()\n",
"plt.tight_layout()\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"id": "96ce2705",
"metadata": {},
"source": [
"This example helps to emphasize that asymptotic stationarity is about the distribution, while ergodicity is about the sample path.\n",
"\n",
"The proportion of time spent in a state can converge to the stationary distribution with periodic chains.\n",
"\n",
"However, the distribution at each state does not."
]
},
{
"cell_type": "markdown",
"id": "19203b49",
"metadata": {},
"source": [
"### Example: political institutions\n",
"\n",
"Let’s go back to the political institutions model with six states discussed [in a previous lecture](https://intro.quantecon.org/markov_chains_I.html#mc-eg3) and study ergodicity.\n",
"\n",
"Here’s the transition matrix.\n",
"\n",
"$$\n",
"P :=\n",
" \\begin{bmatrix} \n",
" 0.86 & 0.11 & 0.03 & 0.00 & 0.00 & 0.00 \\\\\n",
" 0.52 & 0.33 & 0.13 & 0.02 & 0.00 & 0.00 \\\\\n",
" 0.12 & 0.03 & 0.70 & 0.11 & 0.03 & 0.01 \\\\\n",
" 0.13 & 0.02 & 0.35 & 0.36 & 0.10 & 0.04 \\\\\n",
" 0.00 & 0.00 & 0.09 & 0.11 & 0.55 & 0.25 \\\\\n",
" 0.00 & 0.00 & 0.09 & 0.15 & 0.26 & 0.50\n",
" \\end{bmatrix}\n",
"$$\n",
"\n",
"The [graph](https://intro.quantecon.org/markov_chains_I.html#mc-eg3) for the chain shows all states are reachable,\n",
"indicating that this chain is irreducible.\n",
"\n",
"In the next figure, we visualize the difference $ \\hat p_n(x) - \\psi^* (x) $ for each state $ x $.\n",
"\n",
"Unlike the previous figure, $ X_0 $ is held fixed."
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "45f425ae",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"P = [[0.86, 0.11, 0.03, 0.00, 0.00, 0.00],\n",
" [0.52, 0.33, 0.13, 0.02, 0.00, 0.00],\n",
" [0.12, 0.03, 0.70, 0.11, 0.03, 0.01],\n",
" [0.13, 0.02, 0.35, 0.36, 0.10, 0.04],\n",
" [0.00, 0.00, 0.09, 0.11, 0.55, 0.25],\n",
" [0.00, 0.00, 0.09, 0.15, 0.26, 0.50]]\n",
"\n",
"ts_length = 2500\n",
"mc = qe.MarkovChain(P)\n",
"ψ_star = mc.stationary_distributions[0]\n",
"fig, ax = plt.subplots()\n",
"X = mc.simulate(ts_length, random_state=1)\n",
"# Center the plot at 0\n",
"ax.axhline(linestyle='dashed', lw=2, color='black')\n",
"\n",
"\n",
"for x0 in range(len(P)):\n",
" # Calculate the fraction of time for each state\n",
" p_hat = (X == x0).cumsum() / np.arange(1, ts_length+1)\n",
" ax.plot(p_hat - ψ_star[x0], label=f'$x = {x0+1} $')\n",
" ax.set_xlabel('t')\n",
" ax.set_ylabel(r'$\\hat p_n(x) - \\psi^* (x)$')\n",
"\n",
"ax.legend()\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"id": "1ef7f682",
"metadata": {},
"source": [
"## Exercises"
]
},
{
"cell_type": "markdown",
"id": "f28553da",
"metadata": {},
"source": [
"## Exercise 35.1\n",
"\n",
"Benhabib et al. [[Benhabib *et al.*, 2019](https://intro.quantecon.org/zreferences.html#id278)] estimated that the transition matrix for social mobility as the following\n",
"\n",
"$$\n",
"P:=\n",
" \\begin{bmatrix} \n",
" 0.222 & 0.222 & 0.215 & 0.187 & 0.081 & 0.038 & 0.029 & 0.006 \\\\\n",
" 0.221 & 0.22 & 0.215 & 0.188 & 0.082 & 0.039 & 0.029 & 0.006 \\\\\n",
" 0.207 & 0.209 & 0.21 & 0.194 & 0.09 & 0.046 & 0.036 & 0.008 \\\\ \n",
" 0.198 & 0.201 & 0.207 & 0.198 & 0.095 & 0.052 & 0.04 & 0.009 \\\\ \n",
" 0.175 & 0.178 & 0.197 & 0.207 & 0.11 & 0.067 & 0.054 & 0.012 \\\\ \n",
" 0.182 & 0.184 & 0.2 & 0.205 & 0.106 & 0.062 & 0.05 & 0.011 \\\\ \n",
" 0.123 & 0.125 & 0.166 & 0.216 & 0.141 & 0.114 & 0.094 & 0.021 \\\\ \n",
" 0.084 & 0.084 & 0.142 & 0.228 & 0.17 & 0.143 & 0.121 & 0.028\n",
"\\end{bmatrix}\n",
"$$\n",
"\n",
"where each state 1 to 8 corresponds to a percentile of wealth shares\n",
"\n",
"$$\n",
"0-20 \\%, 20-40 \\%, 40-60 \\%, 60-80 \\%, 80-90 \\%, 90-95 \\%, 95-99 \\%, 99-100 \\%\n",
"$$\n",
"\n",
"The matrix is recorded as `P` below"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "cfcada1c",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"P = [\n",
" [0.222, 0.222, 0.215, 0.187, 0.081, 0.038, 0.029, 0.006],\n",
" [0.221, 0.22, 0.215, 0.188, 0.082, 0.039, 0.029, 0.006],\n",
" [0.207, 0.209, 0.21, 0.194, 0.09, 0.046, 0.036, 0.008],\n",
" [0.198, 0.201, 0.207, 0.198, 0.095, 0.052, 0.04, 0.009],\n",
" [0.175, 0.178, 0.197, 0.207, 0.11, 0.067, 0.054, 0.012],\n",
" [0.182, 0.184, 0.2, 0.205, 0.106, 0.062, 0.05, 0.011],\n",
" [0.123, 0.125, 0.166, 0.216, 0.141, 0.114, 0.094, 0.021],\n",
" [0.084, 0.084, 0.142, 0.228, 0.17, 0.143, 0.121, 0.028]\n",
" ]\n",
"\n",
"P = np.array(P)\n",
"codes_B = ('1','2','3','4','5','6','7','8')"
]
},
{
"cell_type": "markdown",
"id": "3c2b6a8b",
"metadata": {},
"source": [
"1. Show this process is asymptotically stationary and calculate an approximation to the stationary distribution. \n",
"1. Use simulations to illustrate ergodicity. "
]
},
{
"cell_type": "markdown",
"id": "27a1c1e0",
"metadata": {},
"source": [
"## Solution to[ Exercise 35.1](https://intro.quantecon.org/#mc_ex1)\n",
"\n",
"Part 1:\n",
"\n",
"One option is to take the power of the transition matrix."
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "96b0a557",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"P = [[0.222, 0.222, 0.215, 0.187, 0.081, 0.038, 0.029, 0.006],\n",
" [0.221, 0.22, 0.215, 0.188, 0.082, 0.039, 0.029, 0.006],\n",
" [0.207, 0.209, 0.21, 0.194, 0.09, 0.046, 0.036, 0.008],\n",
" [0.198, 0.201, 0.207, 0.198, 0.095, 0.052, 0.04, 0.009],\n",
" [0.175, 0.178, 0.197, 0.207, 0.11, 0.067, 0.054, 0.012],\n",
" [0.182, 0.184, 0.2, 0.205, 0.106, 0.062, 0.05, 0.011],\n",
" [0.123, 0.125, 0.166, 0.216, 0.141, 0.114, 0.094, 0.021],\n",
" [0.084, 0.084, 0.142, 0.228, 0.17, 0.143, 0.121, 0.028]]\n",
"\n",
"P = np.array(P)\n",
"codes_B = ('1','2','3','4','5','6','7','8')\n",
"\n",
"np.linalg.matrix_power(P, 10)"
]
},
{
"cell_type": "markdown",
"id": "8746476e",
"metadata": {},
"source": [
"For this model, rows of $ P^n $ converge to the stationary distribution as $ n \\to\n",
"\\infty $:"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "7c7951a5",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"mc = qe.MarkovChain(P)\n",
"ψ_star = mc.stationary_distributions[0]\n",
"ψ_star"
]
},
{
"cell_type": "markdown",
"id": "59f90275",
"metadata": {},
"source": [
"Part 2:"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "225c50ae",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"ts_length = 1000\n",
"mc = qe.MarkovChain(P)\n",
"fig, ax = plt.subplots()\n",
"X = mc.simulate(ts_length, random_state=1)\n",
"ax.axhline(linestyle='dashed', lw=2, color='black')\n",
"\n",
"for x0 in range(len(P)):\n",
" # Calculate the fraction of time for each worker\n",
" p_hat = (X == x0).cumsum() / np.arange(1, ts_length+1)\n",
" ax.plot(p_hat - ψ_star[x0], label=f'$x = {x0+1} $')\n",
" ax.set_xlabel('t')\n",
" ax.set_ylabel(r'$\\hat p_n(x) - \\psi^* (x)$')\n",
"\n",
"ax.legend()\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"id": "8dc51978",
"metadata": {},
"source": [
"Note that the fraction of time spent at each state converges to the probability\n",
"assigned to that state by the stationary distribution."
]
},
{
"cell_type": "markdown",
"id": "86f5bc8b",
"metadata": {},
"source": [
"## Exercise 35.2\n",
"\n",
"According to the discussion [above](#mc-eg1-2), if a worker’s employment dynamics obey the stochastic matrix\n",
"\n",
"$$\n",
"P := \n",
"\\begin{bmatrix} \n",
"1 - \\alpha & \\alpha \\\\\n",
"\\beta & 1 - \\beta\n",
"\\end{bmatrix}\n",
"$$\n",
"\n",
"with $ \\alpha \\in (0,1) $ and $ \\beta \\in (0,1) $, then, in the long run, the fraction\n",
"of time spent unemployed will be\n",
"\n",
"$$\n",
"p := \\frac{\\beta}{\\alpha + \\beta}\n",
"$$\n",
"\n",
"In other words, if $ \\{X_t\\} $ represents the Markov chain for\n",
"employment, then $ \\bar X_m \\to p $ as $ m \\to \\infty $, where\n",
"\n",
"$$\n",
"\\bar X_m := \\frac{1}{m} \\sum_{t = 1}^m \\mathbb{1}\\{X_t = 0\\}\n",
"$$\n",
"\n",
"This exercise asks you to illustrate convergence by computing\n",
"$ \\bar X_m $ for large $ m $ and checking that\n",
"it is close to $ p $.\n",
"\n",
"You will see that this statement is true regardless of the choice of initial\n",
"condition or the values of $ \\alpha, \\beta $, provided both lie in\n",
"$ (0, 1) $.\n",
"\n",
"The result should be similar to the plot we plotted [here](#ergo)"
]
},
{
"cell_type": "markdown",
"id": "82f8f781",
"metadata": {},
"source": [
"## Solution to[ Exercise 35.2](https://intro.quantecon.org/#mc_ex2)\n",
"\n",
"We will address this exercise graphically.\n",
"\n",
"The plots show the time series of $ \\bar X_m - p $ for two initial\n",
"conditions.\n",
"\n",
"As $ m $ gets large, both series converge to zero."
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "8e65ff92",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"α = β = 0.1\n",
"ts_length = 3000\n",
"p = β / (α + β)\n",
"\n",
"P = ((1 - α, α), # Careful: P and p are distinct\n",
" ( β, 1 - β))\n",
"mc = qe.MarkovChain(P)\n",
"\n",
"fig, ax = plt.subplots()\n",
"ax.axhline(linestyle='dashed', lw=2, color='black')\n",
"\n",
"for x0 in range(len(P)):\n",
" # Generate time series for worker that starts at x0\n",
" X = mc.simulate(ts_length, init=x0)\n",
" # Compute fraction of time spent unemployed, for each n\n",
" X_bar = (X == 0).cumsum() / np.arange(1, ts_length+1)\n",
" # Plot\n",
" ax.plot(X_bar - p, label=f'$x_0 = \\, {x0} $')\n",
" ax.set_xlabel('t')\n",
" ax.set_ylabel(r'$\\bar X_m - \\psi^* (x)$')\n",
" \n",
"ax.legend()\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"id": "8c31dc8f",
"metadata": {},
"source": [
"## Exercise 35.3\n",
"\n",
"In `quantecon` library, irreducibility is tested by checking whether the chain forms a [strongly connected component](https://networkx.org/documentation/stable/reference/algorithms/generated/networkx.algorithms.components.is_strongly_connected.html).\n",
"\n",
"Another way to test irreducibility is via the following statement:\n",
"\n",
"The $ n \\times n $ matrix $ A $ is irreducible if and only if $ \\sum_{k=0}^{n-1}A^k $\n",
"is a strictly positive matrix.\n",
"\n",
"(see, e.g., [[Zhao, 2012](https://intro.quantecon.org/zreferences.html#id277)] and [this StackExchange post](https://math.stackexchange.com/questions/3336616/how-to-prove-this-matrix-is-a-irreducible-matrix))\n",
"\n",
"Based on this claim, write a function to test irreducibility."
]
},
{
"cell_type": "markdown",
"id": "cf646ac6",
"metadata": {},
"source": [
"## Solution to[ Exercise 35.3](https://intro.quantecon.org/#mc_ex3)"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "9144b086",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"def is_irreducible(P):\n",
" n = len(P)\n",
" result = np.zeros((n, n))\n",
" for i in range(n):\n",
" result += np.linalg.matrix_power(P, i)\n",
" return np.all(result > 0)"
]
},
{
"cell_type": "markdown",
"id": "1b5ec3b1",
"metadata": {},
"source": [
"Let’s try it."
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "d09043e8",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"P1 = np.array([[0, 1],\n",
" [1, 0]])\n",
"P2 = np.array([[1.0, 0.0, 0.0],\n",
" [0.1, 0.8, 0.1],\n",
" [0.0, 0.2, 0.8]])\n",
"P3 = np.array([[0.971, 0.029, 0.000],\n",
" [0.145, 0.778, 0.077],\n",
" [0.000, 0.508, 0.492]])\n",
"\n",
"for P in (P1, P2, P3):\n",
" result = lambda P: 'irreducible' if is_irreducible(P) else 'reducible'\n",
" print(f'{P}: {result(P)}')"
]
}
],
"metadata": {
"date": 1750037600.8396378,
"filename": "markov_chains_II.md",
"kernelspec": {
"display_name": "Python",
"language": "python3",
"name": "python3"
},
"title": "Markov Chains: Irreducibility and Ergodicity"
},
"nbformat": 4,
"nbformat_minor": 5
}